What about that point? Just let it float, duh
IEEE standard for floats [Number System 3]
This piece presents an utterly complicated topic - IEEE754 Standard - in its distilled form, so it's relatively short. I've been prohibited from sharing any of the problems from my lab sessions. Apologies for that. But I've tried hard to subside the fog of confusion around this topic. Enjoy!
** 📱users, go landscape for a better reading experience.
Setting up the stage
Let's jump right in.
We know for a fact that the sum of 0.1 and 0.2 is 0.3, but our computers don't really reckon with it. In any programming language, the sum resembles 0.300...4, which is downright weird. Similarly, the output for (2.3 - 2.2) is 0.099...64, which is anything but a complete 0.1 - the "math" answer. For proof, check this JS-console snap👇
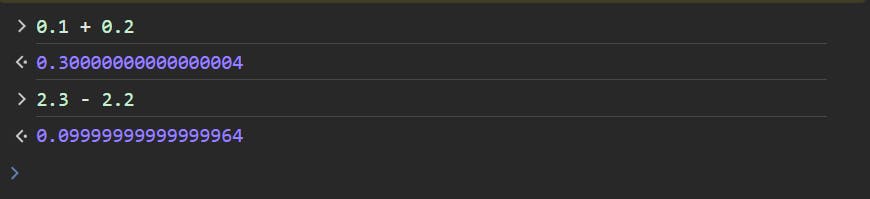
Things are equally weird for a fraction whose float-equivalent has a recurring mantissa. For instance, the float for \(10/3\) is \(3.\bar{3}\), but a machine is incapable of just putting a 'bar' on the recurring digit. The following shot shows the actual computer outputs:
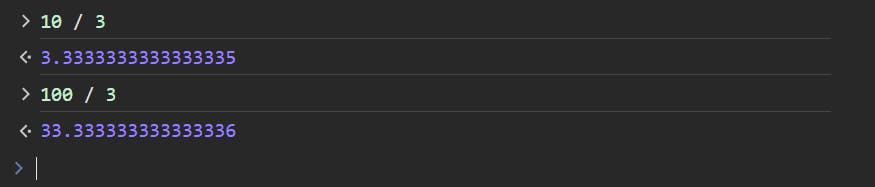
Strange, ain't it? Essentially,
Machines do arithmetic differently than us humans.
Hardware's the real culprit
IEEE754, in simple words, is a set of rules that a processor strictly obeys whilst dealing with floating-point numbers. It's a technical standard that every hardware maker has to comply with. This article elucidates one of the floating-point formats that the standard defines, namely, 32-bit (single precision).
Single precision
Consider -17.2, a decimal. Let's determine its binary in 32-bit IEEE format.
Step 1: Convert the given decimal into binary as usual. Ignore the "sign" for now, it'll be taken care of in the last step.
Exponent: 10001
Mantissa: 00110011001100110011...
---------------------------------------
Binary: 10001 . 00110011001100110011...
Step 2: Represent the obtained binary in scientific notation.
In scientific notation, a float binary is written so that it begins with "1." To fulfill this criteria, the point must be shifted 4 places to the left in the obtained binary.
After bit-shifting, we have
1 . 000100110011001100110011... x 2^4
Step 3: Convert the scientific notation into IEEE format.
In single precision format, IEEE allows only 32 bits to store a float. Of those bits, one is reserved for sign, and eight for exponent. Hence, we have 23 bits to store the precision (mantissa) of a float.

So we need to represent the above exponent (4) in 8-bit binary. As per IEEE rules, a bias must be added to the exponent, and the resultant be then converted into binary. In 32-bit format, the bias is 127; hence,
Exponent = 127 + 4 = 131
Binary of 131: 1000 0011
Now, we're ready to represent the above binary in single precision IEEE format.
N.B.
At this point, we look at the given number's magnitude, and put 0 or 1 accordingly for the sign-bit.
As mentioned earlier, we only consider 23 bits for mantissa, but there's a catch. If the 24th bit is 1, then the final answer must be rounded, which simply means adding 1 to it. For instance, the answer below has been rounded.
╔══════╦══════════╦═════════════════════════╗
║ Sign ║ Exponent ║ Mantissa ║
╠══════╬══════════╬═════════════════════════╣
║ 1 ║ 10000011 ║ 00010011001100110011010 ║
╚══════╩══════════╩═════════════════════════╝
Answer: 11000001100010011001100110011010
** If you have trust issues, you can cross-check it using this IEEE 754 calculator.
Bonus: Double precision
In double precision format, IEEE allows 64 bits to store a float. The distribution of bits is illustrated below:

The steps to determine the double precision binary of a given decimal are pretty similar to those involved in single precision. The only differences are listed below:
In 64-bit format, the bias is 1023.
When truncating the mantissa to 52 bits, notice the 53rd bit. If it's 1, the final answer must be rounded.
The key
The computer stores the binary, 11000001100010011001100110011010, for -17.2, but that's not how it's showed to us. During output, that binary is converted back to decimal, which doesn't turn out to be a complete -17.2, but something close to it.
I'm not at liberty to demonstrate the cross-verification process, but I hope I was able to provide a little clarification.
Grateful to Ozh for the ASCII art
Thank You!
Plz like and share😊