Some of the available information regarding C data types is incorrect. In this piece, I'm offering a method to get to the correct values for a few of them, but the process is similar for the rest.
Enjoy!✌
Data types
A data type determines the set of values a data item (like a variable) can take and the operations that can be performed on it. The C language offers four basic data types, namely, char , int , float , and double
Our textbooks say that the sizes and ranges for each type are as follows:
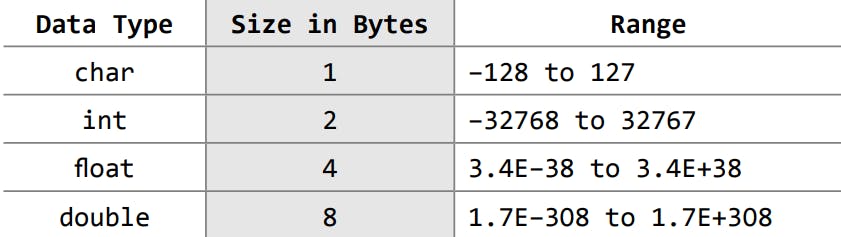
But parts of the above data are WRONG!
int
Size
We can use the sizeof operator to find the size of each data type:
printf("%ld bytes\n", sizeof(int)); // Out: 4 bytes
printf("%ld bytes\n", sizeof(unsigned int)); // Out: 4 bytes
As per the compiler, the size of the int data type and its unsigned variant is 4 bytes, not 2.
Most modern PCs use 64-bit architecture, whereas the data in the books have been recorded using 32-bit machines.
Range
By default, the basic types deal with signed values. We can find the range of int as follows:
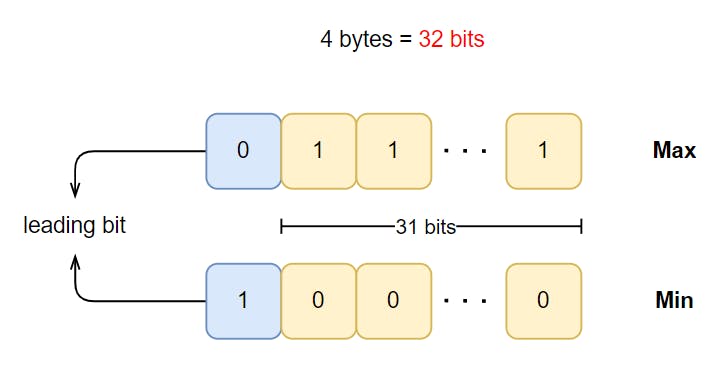
Therefore, the max and min values for the int type is:
$$\sum\limits_{n=0}^{30} 2^n = 2147483647$$
$$-2^{31} = -2147483648$$
For the unsigned int type, there is no sign bit, so we can fill all the "boxes" with 1's for the max value, and 0's for the min value. Thus, the range for unsigned int is from 0 to
$$\sum\limits_{n=0}^{31} 2^n = 4294967295$$
** The above can be used to find the sizes and ranges of all the variants of the int data type.
The range for floats
Since the size of float is 4 bytes, floats are stored in the IEEE754 single-precision format.
How do we find the biggest and the smallest float value?
We know that in the single-precision format, 1 bit is for the sign, 8 bits are for the exponent, and 23 bits are reserved for the significand (mantissa). Therefore, for the max value, the exponent and the mantissa should be at their max - all 1's, and for the min value, they should be all 0's. But ...

It's not that simple!
In IEEE, certain bit patterns are reserved for some special values:
+Inf: exponent – all 1’s (255), mantissa – zero.
-Inf: exponent – all 1’s (255), mantissa – zero, and sign – 1.
NaN: exponent – all 1’s (255), mantissa – non-zero.
Zero: exponent – zero, mantissa – zero.
Denormalised num: exponent – zero, mantissa – non-zero.
For ordinary numbers, exponent varies from 00000001 to 11111110 in single precision. The range is similar for higher precisions.
To verify, use this calculator
Minimum
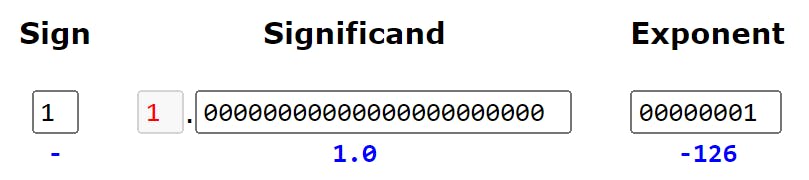
Exponent: Stored exp - Bias = 1 - 127 = -126
Forumula to find the Decimal:
(-1)^sign x (1 + mantissa) x 2^(exponent)
= (-1)^1 x 1.0 x 2^(-126)
= -0.0000000000000000000000000000000000000117
= -1.17E-38
Maximum
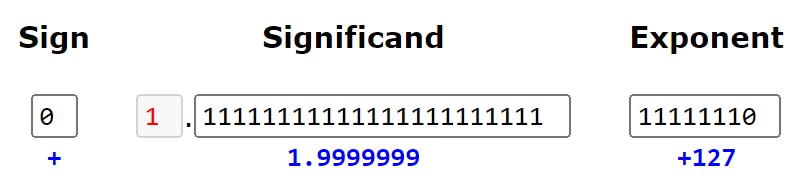
Exponent: Stored exp - Bias = 254 - 127 = 127
Decimal:
(-1)^sign x (1 + mantissa) x 2^(exponent)
= (-1)^0 x 1.9999998807907104 x 2^(127)
= 340282346638528851437567810039546926146.01
= 3.4E+38
** We can use the same procedure the find the respective ranges of double and long double data types.
Thank you! ☺
Plz like and share💜